گراف چیست؟
یک گراف (نمودار) را می توان به عنوان یک ساختار داده در نظر گرفت که هدف آن توصیف روابط بین موجودیت ها می باشد. موجودیت می تواند هر چیزی باشد که دارای وجه متمایز و مستقل است. موجودیت می تواند یک شی فیزیکی واقعی یا یک ایده انتزاعی باشد. به عنوان مثال، یک موجودیت می تواند یک شخص، مکان یا سازمانی باشد که داده ها را می توان با آن ذخیره کرد.
در دنیای محاسبات، گراف ها به دلیل توانایی آنها نه تنها در ارائه انتزاعات به زندگی واقعی بلکه جهت نشان دادن روابط پیچیده به راحتی از آن استفاده می شود. به این ترتیب، انواع مسائل عملی را می توان به صورت گراف نشان داد. به عنوان مثال، یک ساختار پیوندی از وب سایت ها را می توان به عنوان یک گراف مشاهده کرد.
هر گراف مجموعه ای از نقاط است که به عنوان راس یا گره نامیده می شوند و با استفاده از خطوطی به نام یال به هم متصل می شوند . رئوس موجودیت های موجود در یک گراف را نشان می دهد. از طرف دیگر لبه ها یا همان یال ها روابط بین موجودیت ها را بیان می کنند. از این رو، یک گراف G با مجموعه ای از رئوس V به همراه مجموعه ای از یال های E به صورت G= (V, E) نمایش داده می شود. هم رئوس و هم یال ها می توانند ویژگی های اضافی داشته باشند که برای توصیف موجودیت ها و روابط آن ها استفاده می شوند. شکل 1 یک نمودار ساده با پنج گره و شش یال را نشان می دهد.
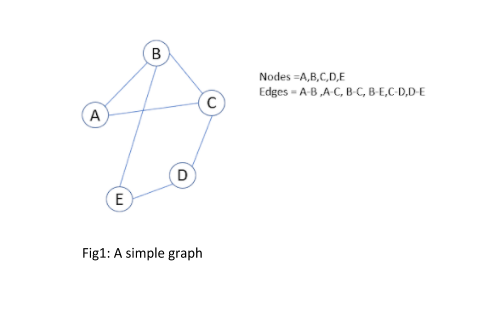
شکل 1) یک گراف ساده
در کاربردهای واقعی گراف ها، یک لبه ممکن است نشان دهنده روابط بین افراد در لینکدین یا یک رابطه شخصی در یک پلت فرم رسانه های اجتماعی مانند فیس بوک یا اینستاگرام باشد.
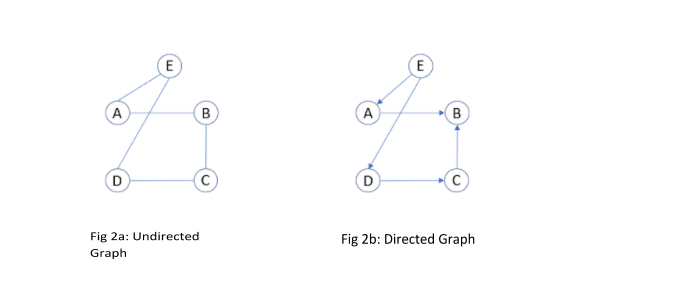
انواع گراف
به طور کلی گراف ها را می توان به غیر جهت دار (شکل 2a) یا جهت دار (شکل 2b) دسته بندی کرد. در گراف بدون جهت جهت یال ها مهم نیست. بدان معنی است که لبه ها هیچ جهتی ندارند. به عبارت دیگر، رابطه متقابل است. به عنوان مثال، مانند یک ارتباط در فیس بوک یا لینکدین به صورت دو طرفه است یعنی هر فرد با هر شخص دیگری در شبکه دوست باشد آن فرد هم متقابلا با او دوست است. اما، لبه های گراف های جهت دار دارای جهت های مرتبط با آنها هستند. یک رابطه نامتقارن بین رئیس و کارمند یا معلم و دانش آموز را می توان به عنوان یک نمودار جهت دار در ساختار داده نشان داد. گراف ها همچنین می توانند وزن داشته باشند (شکل 2c) مقادیر واقعی مرتبط با لبه ها را نشان می دهد. بسته به کاربرد خاص گراف، وزن لبه ممکن است مقادیری مانند فاصله، هزینه، شباهت و غیره را نشان دهد.
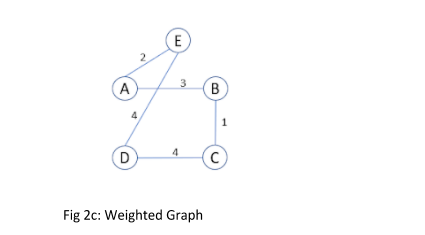
گراف وزن دار
انواع نمایش گراف
یک گراف را می توان با استفاده از 3 ساختار داده نشان داد:
- ماتریس مجاورت
- لیست مجاورت
- مجموعه مجاورت
ماتریس مجاورت را می توان به عنوان جدولی با سطرها و ستون ها در نظر گرفت. برچسب های ردیف و برچسب های ستون گره های یک گراف را نشان می دهند. ماتریس مجاورت یک ماتریس مربع است که در آن تعداد سطرها، ستون ها و گره ها یکسان است. هر سلول ماتریس یک یال یا رابطه بین دو گره داده شده را نشان می دهد. به عنوان مثال، ماتریس مجاورت Aij تعداد پیوندها از i به j را با توجه به دو گره i و j نشان می دهد.
| A | B | C | D | E | |
| A | 0 | 0 | 0 | 0 | 1 |
| B | 0 | 0 | 1 | 0 | 0 |
| C | 0 | 1 | 0 | 0 | 1 |
| D | 1 | 0 | 0 | 1 | 0 |
| E | 0 | 1 | 1 | 0 | 0 |
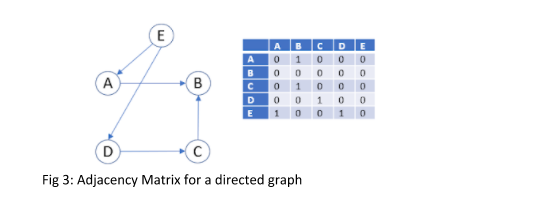
ماتریس مجاورت برای یک گراف جهت دار در شکل 3 نشان داده شده است. توجه کنید که این ماتریس مربعی است که در آن تعداد سطرها، ستون ها و گره ها یکسان است. هر سطر و ستون مربوط به یک گره یا یک رأس یک گراف است. سلول های درون ماتریس نشان دهنده ارتباطی است که بین گره ها وجود دارد. از آنجایی که در گراف جهت دار داده شده، هیچ گره ای به خودش متصل نیست، تمام سلول های واقع در مورب ماتریس صفر علامت گذاری می شوند. برای بقیه سلول ها، اگر یک یال جهت دار از یک گره معین به گره دیگر وجود داشته باشد، آنگاه سلول مربوطه با یک عدد دیگر صفر مشخص می شود.
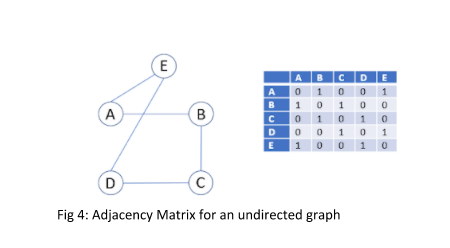
برای درک اینکه چگونه یک گراف بدون جهت را می توان با استفاده از یک ماتریس مجاورت نشان داد، یک گراف کوچک بدون جهت با پنج راس را در نظر بگیرید (شکل 4). در اینجا، A به B متصل است، اما B نیز به A متصل است. از این رو، هر دو سلول یعنی یکی با منبع A مقصد B و دیگری با منبع B مقصد A علامت گذاری می شوند. که نیاز به یک لبه بدون جهت کافی است. توجه کنید که ورودی دوم در یک مکان آینه ای در سراسر مورب اصلی قرار دارد.
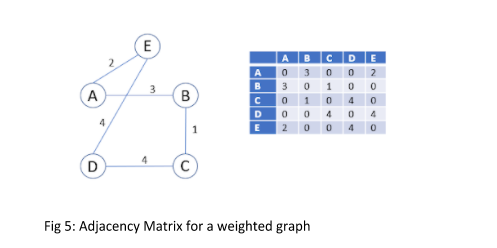
در مورد گراف وزن دار، سلول ها به جای وزنه های لبه علامت گذاری می شوند. در شکل 5، وزن تخصیص داده شده به گره های اتصال لبه B و D برابر با 3 است. بنابراین، سلول های مربوطه در ماتریس مجاورت یعنی ردیف B ستون D و ردیف D ستون B با علامت 3 مشخص می شوند.
کتابخانه NetworkX یک روش آسان برای ایجاد ماتریس های مجاورت ارائه می دهد. مثال زیر نشان می دهد که چگونه می توانیم با استفاده از NetworkX یک ماتریس مجاورت اولیه ایجاد کنیم.

در نمایش لیست مجاورت یک گراف، هر راس به عنوان یک شی گره نشان داده می شود. گره ممکن است حاوی داده یا ارجاع به یک لیست پیوندی باشد. این لیست پیوندی فهرستی از تمام گره هایی که در مجاورت گره فعلی هستند را ارائه می دهد. نموداری را در نظر بگیرید که حاوی یک لبه اتصال گره A و گره B است. سپس، گره A در لیست پیوندی گره B در دسترس خواهد بود. شکل 6 یک نمودار نمونه از 5 گره و لیست مجاورت مربوط به آن را نشان می دهد.
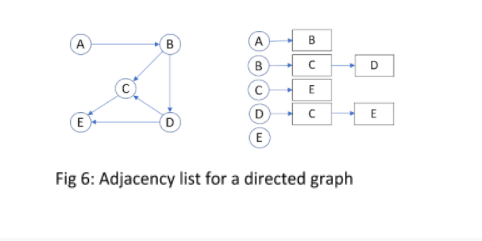
توجه داشته باشید که لیست مربوط به گره E خالی است در حالی که لیست های مربوط به گره های B و D هر کدام دارای 2 ورودی هستند.
به طور مشابه، لیست های مجاورتی برای یک گراف بدون جهت نیز می توانند ساخته شوند. شکل 7 نمونه ای از یک گراف بدون جهت را به همراه فهرست مجاورت آن برای درک بهتر ارائه می دهد.
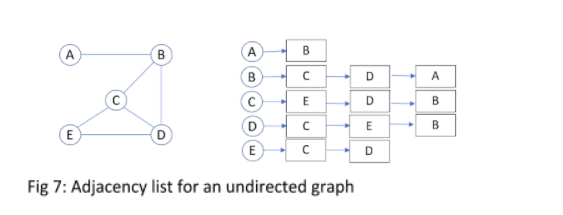
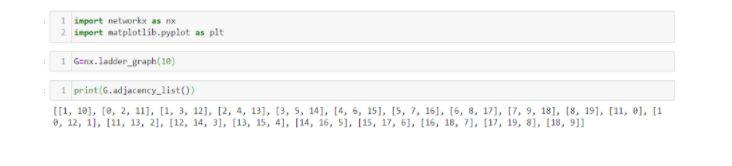
لیست مجاورت فرآیند جستجوی سریعتر را در مقایسه با ماتریس مجاورت امکان پذیر می کند. با این حال، بازهم نمی توان گفت که بهترین نمایش گراف ها است، به خصوص در مورد اضافه کردن یا حذف گره ها. به عنوان مثال، حذف یک گره شامل بررسی تمام لیست های مجاورت برای حذف یک گره خاص از همه لیست ها می شود. کتابخانه NetworkX یک تابع adjacency_list () را برای تولید لیست مجاورت یک گراف ارائه می دهد. کد زیر کاربرد آن را نشان می دهد.
مجموعه مجاورت تعدادی از چالش های ایجاد شده توسط لیست مجاورت را کاهش می دهد. مجموعه مجاورت کاملاً شبیه به لیست مجاورت است با این تفاوت که به جای لیست پیوندی. مجموعه ای از رئوس مجاور ارائه شده است. لیست و مجموعه مجاورت اغلب برای نمودارهای پراکنده با اتصالات کمی بین گره ها استفاده می شود. برعکس، ماتریس مجاورت برای گرافهایی که به خوبی متصل هستند و گرههای زیادی را شامل میشوند، به خوبی کار میکند.

